Data and Software Security
The protection of data and programs used in computer system is known as software security.This note provides an information about data and software security.
Summary
The protection of data and programs used in computer system is known as software security.This note provides an information about data and software security.
Things to Remember
- The protection of data and programs used in computer system is known as software security.
- Some common software security are Password Protection, Backup System, Defragmentation, Hard Lock Key, Virus Scanning, Scandisk and Using a firewall.
- A password is a secret word or phrase that provides uses access to a particular program system.
- Backup means to store some copy of programs, operating system, compilers, data, information, etc. permanently in secondary storage devices like hard disk, floppy disk, etc.
- Defragmentation is the process of rewriting part of a file to contiguous sector on hard disk to increase the speed of processing.
- Some software use hard lock key which is connected to one of the ports of the computer.
- Scandisk is a process, which analyzes and repairs logical and physical disk errors like files, folders, bad sectors and lost chains.
- A firewall's main purpose is to prohibit unauthorized access to your computer via the internet.
MCQs
No MCQs found.
Subjective Questions
Q1:
In the figure , AB = 8cm and the distance from centre O to the chord bc is 3 cm. If the radius of the circle = 5 cm , prove that AB = BC.

Type: Short Difficulty: Easy
Q2:
In the figure O is the centre of the circle and OM⊥AB and ON ⊥ CD. Find the length of AB.

Type: Short Difficulty: Easy
Q3:
In the figure , O is the center of cirlce. IF OB = 13cm , CD = 24cm , what will be the value of x ?
Type: Short Difficulty: Easy
Q4:
In the figure , O is the centre of the circle. If OE = 17cm , OD = 8cm , what is the length of chord BC ?
Type: Short Difficulty: Easy
Q5:
In a circle having radius 25cm , a chord is drawn at the distance if 24 cm from the centre. Find the length of the chord.

Type: Short Difficulty: Easy
Q6:
In a circle , a chord of length 12 cm is 8 cm away from the centre. Find the radius of the circle.

Type: Short Difficulty: Easy
Q7:
Find the length of chords whose distance from the centre of radius 25 cm are:
(i) 20 cm (ii) 7 cm
Type: Long Difficulty: Easy
Q8:
Prove thet
In the given figure , O is the centre of the circle. If OPA = DPO , prove thet AB = CD
Type: Short Difficulty: Easy
Q9:
In the given figure , O is the centre . If PQ = RS , prove that OM bisects PMS.
Type: Short Difficulty: Easy
Q10:
In the given figure , O is the common centre of both circles. Chord MN cuts the small circle at points R and S Prove that MR = NS.
Type: Short Difficulty: Easy
Videos
NCEA Maths Level 1 Geometric Reasoning: Angles Within Circles
CIRCLE GEOMETRY (THEOREMS AND THEIR APPLICATION)
Circles: radius, diameter, circumference and Pi | Geometry | Khan Academy

Data and Software Security
The protection of data and programs used in computer system is known as software security. Software security provides barriers and other cyber-tools that protect programs, files, operating systems and the information flow to and from a computer.
Some common software security are:

1. Password Protection
A password is a secret word or phrase that provides uses access to a particular program system. Every software enable you to password-protect a variety of resources. If you use any network features, you should password protect them frequently. Experts advise that you use long password and do not use long passwords that could be easily guessed. Never use blank password.

2. Backup
Backup means to store some copy of programs, operating system, compilers, data, information, etc. permanently in secondary storage devices like hard disk, floppy disk, etc. A simple disk error can do just as much damage as a hacker might do. And even the most experienced computer user occasionally deletes a file or folder by accident. So, backup is very essential.
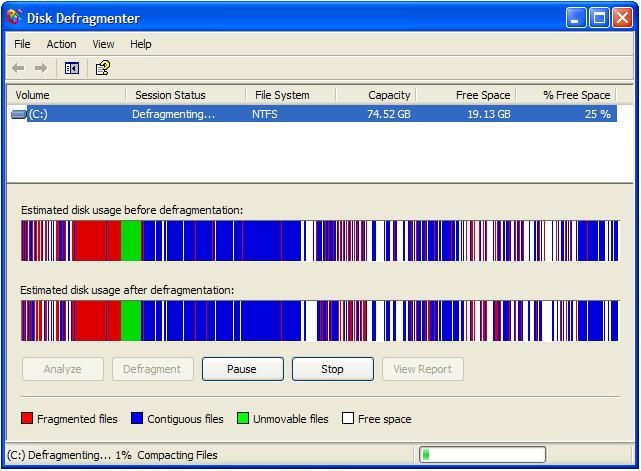
3. Defragmentation
Defragmentation is the process of rewriting part of a file to contiguous sector on hard disk to increase the speed of processing. As you update your data files over time, they may become fragmented, or divided up into several widely spaced pieces. This can slow down data retrieval if the problems become severe. Using a defragmenter can restore that lost performance.

4. Hard Lock Key
Some software use hard lock key which is connected to one of the ports of the computer. When software is executed it checks for hard lock. If the hard lock key is absent then the software does not execute. This protects the software from pirated use.

5. Virus scanning
Computer viruses are the most effective factor of data and software. Virus may damage our data and software. Virus produces several unusual symptoms in our computer and gives trouble to the user while working with computer. So, we should keep our computer free from virus. For that we should scan our computer regularly using latest and updated anti -virus software.

6. Scandisk
Scandisk is a process, which analyzes and repairs logical and physical disk errors like files, folders, bad sectors and lost chains. It can fix errors on commonly-used data storage devices.

7. Using a Firewall
A firewall's main purpose is to prohibit unauthorized access to your computer via the internet. A functioning firewall is your best defense against hackers or anyone else who might try to reach your PC via the internet. There are various kinds of firewalls both hardware and software and they can use different methods to keep intruders way from your system.
Lesson
Computer Security
Subject
Computer Science
Grade
Grade 10
Recent Notes
No recent notes.
Related Notes
No related notes.