Cone
A cone is a solid object whose base is a circle and another part is a smooth curved surface that symmetrically ends at a point in space. The point is called the vertex of the cone. The line segments that joins the centre of the base and the vertex is called the height of the cone. Line segments that joins the vertex to the point of the circumference of the base circle is called the generator. The length of the generator is called the slant height of the cone. If the axis is perpendicular to the base of circ
Summary
A cone is a solid object whose base is a circle and another part is a smooth curved surface that symmetrically ends at a point in space. The point is called the vertex of the cone. The line segments that joins the centre of the base and the vertex is called the height of the cone. Line segments that joins the vertex to the point of the circumference of the base circle is called the generator. The length of the generator is called the slant height of the cone. If the axis is perpendicular to the base of circ
Things to Remember
In our context, the cone is right circular cone only.
Total surface area of the cone = \(\pi\)r(i + r) square on
Curbed surface area (CSA) = \(\pi\)rl
MCQs
No MCQs found.
Subjective Questions
Q1:
Write the name of the solid Figures.

Type: Short Difficulty: Easy
Q2:
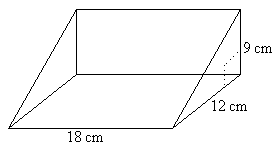
Find the volume of given triangular prism.

Type: Short Difficulty: Easy
Q3:
Find the volume of given triangular prism.

Type: Short Difficulty: Easy
Q4:
Find the volume of given triangular prism.

Type: Short Difficulty: Easy
Q5:
Find the volume of given triangular prism.
Type: Short Difficulty: Easy
Q6:
Find the volume of given triangle.

Type: Short Difficulty: Easy
Q7:
Find the volume of given triangular prism.

Type: Short Difficulty: Easy
Q8:
Volume of given triangular prism is 42cm3, AC = 4cm and DE = 3cm, find the height of the prism.

Type: Short Difficulty: Easy
Q9:
Find the lateral surface area of the given triangulate prism.

Type: Short Difficulty: Easy
Q10:
Find the lateral surface area of the given triangulate prism.

Type: Short Difficulty: Easy
Q11:
Find the lateral surface area of given triangulate prism.

Type: Short Difficulty: Easy
Q12:
Find the total surface area of the given triangular prism where AB = 5cm, BC = 12cm, CC' = 30cm and \(\angle\)B = 90o

Type: Short Difficulty: Easy
Videos
No videos found.

Cone
Solid objects, as shown below are the cones.


As we see above, a cone is a solid object whose base is a circle and another part is a smooth curved surface that symmetrically ends at a point in space. The point is called the vertex of the cone. The line segments that joins the centre of the base and the vertex is called the height of the cone. Line segments that join the vertex to the point of the circumference of the base circle are called the generator. The length of the generator is called the slant height of the cone. If the axis is perpendicular to the base of the circle is called the generator. The length of the generator is called the slant height of the cone. If the axis is perpendicular to the base circle the cone is called right circular cone. The surface beside the base circle is called the curved surface of the cone. A right circular cone can be formed by rotating a right angled triangle along with its vertical height.
Surface area of a cone

The cone can be formed from the sector of a circle. In the figure given below, a sector of the circle joining along its cut edges.
In this case, the curved surface area of the cone is equal to the area of the sector of the circle.
Here, \begin{align*} \text {radius of circle} &= l \: units \\ \text {Central angle} &= \theta \\ \text {Arc length} &= 2 \pi r\\ \text {Where r} &= \text {radius of base circle} \end{align*}
[ Circumference of base circle of a cone is equal to the length of the sector. ]
We know,
\begin{align*} \theta &= \frac {2 \pi r} {l} \left[ \theta = \frac {l} {r} , l = 2 \pi r, r = l \right] \\ Also, \\Area \: of \: sector &= \frac {\theta \pi l^2}{2 \pi}\\ &= \frac {\theta \pi l^2} {2 \pi} [ \because 360º = 2 \pi ^c , \theta ^c = central \: angle ] \\ &= \frac {\theta l^2} {2} \\ &= \frac {2 \pi r} {l} . \frac {l^2} {2} [\because \theta = \frac {2 \pi r} {l} ] \\&= \pi r l \end{align*}
Therefore, curved surface area of the cone (CSA) =πrl square units, where r is the radius of the base and l is the slant height of cone.
Alternatively,

We can demonstrate the following materials in the classroom to show the curved surface area of the cone. Take a cone and color the curved surface area of the cone by any indices having equal parts. Take the half circle whose radius is equal to the slant height of the cone. The radius of the base circle is r. Roll the cone above the half circle such that vertex of the cone is fixed at the center of a half-circle. One complete roll of cone exactly fits in half circle. In this case, the area of half circle is equal to the curved surface area of the cone. Since the radius of the half circle is same as the slant height of the cone, so that area of half circle is \( \frac {\pi l^2} {2} \) square units.
From above experiment was see that circumference of the base circle with radius r units is equal to the circumference of half circle with radius l units.
i.e. \begin{align*} 2 \pi r &= \pi l \\ or, l &= \pi r \\ or, r &= \frac {l} {2} \end{align*}
\begin{align*} \therefore Area \: of \: half \: circle &= \frac {\pi l^2} {2} sq. \: units \\ &= \pi \frac {l} {2} . l \: sq. \: units \\ &= \pi r l \: sq. \: units \end{align*}
Hence, Curved surface area of cone ( CSA ) =πrl square units.
Total surface Area of the cone (TSA) = CSA + area of circular base.
i.e. \begin{align*} TSA &= CSA + A_b \\ &= \pi r l + \pi r^2 \\ \pi r \: (l + r) and \:l^2 &= h^2 + r^2 \\ &=\pi rl\end{align*}
There 'h' is the height of the cone, l is the slant height of the cone and 'r' is the radius of base circle.
Curved surface area of cone can also be illustrated by the following activities
Let's take a hollow cone made up of paper. Cut the cone along its slant height. We get a sector of a circle whose radius is l units and arc length 2πr units as shown above in the last figure. The last figure is now approximate rectangle whose length is half of 2πr and breadth is l units.
i.e. Length =πr
Breadth = l
\begin{align*} Area \: of \: rectangle \: (A) = l \times b \\ &= \pi r \times l \\ &= \pi r l \: square \: units \end{align*}
\( \therefore \text {Curved surface area of cone} (A) = \pi r l \)
where l = slant height
r = radius of the base circle
Volume of a cone

A cone is a circular pyramid. As we know the volume of a pyramid is one-third of the base area times height. So, this fact can be generalized in case of cone also. Therefore, the volume of a cone is one-thirdof the base area times height.
i.e. \begin{align*} \text {Volume of cone} (v) &= \frac {1} {3} \times base\: area \times height \\ V &= \frac {1} {3} \pi r^2 h \\ \end{align*}
Where r is the radius of the base and h is the height of the cone.
Alternatively,
Take a conical pot whose radius is 'r' units and height are 'h' units. Take a measuring cylinder having the radius of base r units and height h units. Fill the cylinder with water from full of a cone. The water which filled the circular cylinder of radius 'r' and height 'h' could also fill exactly three conical pots of the radius 'r' and height 'h'.
From the above experiment, we conclude that volume of a right circular cone of radius 'r' and height 'h' is one-third of the volume of a right circular cylinder of the same radius and height.
\begin{align*} \text{Volume of a cone} &= \frac {1} {3} \times base \: area \times height \\ &= \frac {1} {3} \pi r^2 \times h \\ &= \frac {1} {3} \pi r^2 h \: cubic \: units \end{align*}
where r = radius of base circle, h = height of cone .
Lesson
Mensuration
Subject
Compulsory Mathematics
Grade
Grade 10
Recent Notes
No recent notes.
Related Notes
No related notes.